২০২১ সালের ৯ম শ্রেণির ৩য় সপ্তাহের উচ্চতর গণিত (Higher Math) অ্যাসাইমেন্ট প্রশ্ন
তোমাদের জন্য নবম শ্রেণির উচ্চতর গণিত বইয়ের প্রথম অধ্যায়, সেট ও ফাংশন থেকে ২০২১ সালের তৃতীয় অ্যাসাইনমেন্ট এর নির্ধারিত কাজটি দেওয়া হয়েছে।
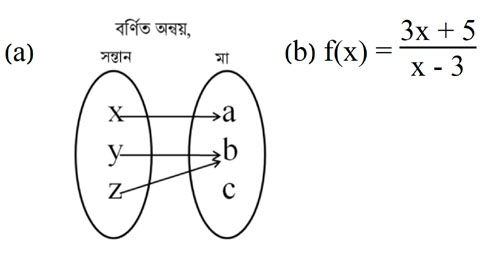
- (ক) বর্ণিত অন্বয়টি ফাংশন হলে তা কী ধরনের ফাংশন যুক্তিসহ উল্লেখ কর।
- (খ) (a) এর বিপরীত ফাংশন সম্ভব কিনা তা যুক্তিসহ উপস্থাপন কর।
- (গ) (b) এর ক্ষেত্রে x ≠ 3 এর জন্য ফাংশনটি এক-এক এবং সার্বিক কিনা তা যুক্তি দিয়ে নিজস্ব মতামত উপস্থাপন কর।
নির্দেশনা: উচ্চতর গণিত পাঠ্য বইয়ের প্রথম অধ্যায়ে আলােচিত সেট ও ফাংশন সম্পর্কে সম্যক ধারণা নিয়ে সমস্যাগুলাে সমাধান করতে বলা হয়েছে।
৯ম শ্রেণির ৩য় সপ্তাহের উচ্চতর গণিত (Higher Math) অ্যাসাইমেন্ট এর নমূনা উত্তর
শতভাগ মূল্যায়ন নির্েদশনা অনুসরণ করে তোমাদের জন্য ২০২১ সালের নবম শ্রেণির তৃতীয় সপ্তাহের উচ্চতর গণিত (Higher Math) সমাধান দেওয়া হল।
উদ্দীপক

প্রশ্ন-(ক): বর্ণিত অন্বয়টি ফাংশন হলে তা কী ধরনের ফাংশন যুক্তিসহ উল্লেখ কর
ক এর সমাধান:
বর্ণিত অন্বয়টি ফাংশন হলে, তা হবে সার্বিক ফাংশন। কারণ, ফাংশনটির অধীনে X→a, Y→b, Z→c।
প্রশ্ন-(খ): (a) এর বিপরীত ফাংশন সম্ভব কিনা তা যুক্তিসহ উপস্থাপন কর
খ এর সমাধান:
মনে করি,
f : A → B একটি এক-এক ও সার্বিক ফাংশন। [সন্তান = A , মা = B ধরি]
একটি ফাংশন g : B → A বর্ণিত হয় যেখানে প্রত্যেক b Є B এর জন্য g(b) = a যদি ও কেবল যদি f(a) = b হয়। এই ফাংশন g কে f এর বিপরীত ফাংশন বলা হয় এবং f-1 দ্বারা নির্দেশ করা হয় অর্থাৎ, g = f-1।
উপরের চিত্রের বর্ণিত ফাংশনটি f হলে f-1 : B → A এবংf-1(a) = X, f-1(b) = Y, f-1(b) = Z ; যা অসম্ভব
অতএব, (a) এর বিপরীত ফাংশন সম্ভব নয়
প্রশ্ন-(গ): (b) এর ক্ষেত্রে x ≠ 3 এর জন্য ফাংশনটি এক-এক এবং সার্বিক কিনা তা যুক্তি দিয়ে নিজস্ব মতামত উপস্থাপন কর
সমাধান:

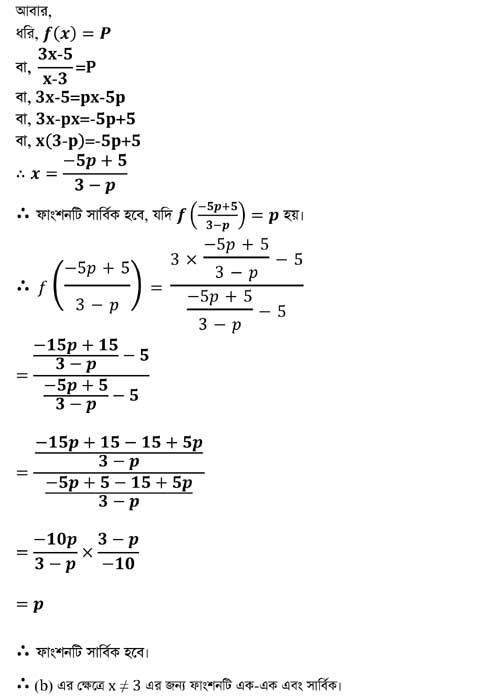
- বাংলাদেশের সংস্কৃতিকে সমৃদ্ধ করার জন্য শিল্পকলা চর্চা গুরুত্বপূর্ণ কেন?
- ৬ষ্ঠ থেকে ৯ম শ্রেণির শিক্ষার্থীদের চলমান অ্যাসাইনমেন্ট কার্যক্রম স্থগিত
- 1st, 2nd and 3rd week assignment class: 8 all Subject 2021
- ৬ষ্ঠ থেকে ৯ম শ্রেণির ৩য় সপ্তাহের অ্যাসাইনমেন্ট উত্তর 2021
- ১ম ২য় ও ৩য় সপ্তাহের সমাধান ২০২১ এসাইনমেন্ট উত্তর ৯ম শ্রেণির
- class: 9 assignment answers 1st/2nd/3rd week assignment answers 2021
- ৮ম শ্রেণির ১ম,২য় ও ৩য় সপ্তাহের এসাইনমেন্ট উত্তর সমূহ ২০২১
- 1st, 2nd and 3rd week assignment class: 8 all Subject 2021
- Class: 7 Assignment Answers 1st, 2nd and 3rd Week Assignment Answers 2021
- ১ম ২য় ও ৩য় সপ্তাহের সমাধান ২০২১ এসাইনমেন্ট উত্তর ৭ম শ্রেণির
- Class 6 Assignment Answer 2021 (1st/2nd/3rd Week) assignment answers 2021
- ৬ষ্ঠ শ্রেণির ১ম,২য় ও ৩য় সপ্তাহের এসাইনমেন্ট উত্তর সমূহ ২০২১
- Class 9 Assignment Answer 2021 All Subject 3rd Week Assignment Solution 2021
- Class: 9 Agricultural Assignment Answer 3rd Week Assignment Solution 2021
- ৯ম শ্রেণি কৃষি শিক্ষা অ্যাসাইনমেন্ট উত্তর ৩য় সপ্তাহের অ্যাসাইনমেন্ট সমাধান 2021
